Calculus Series Cheat Sheet - If there exists some n such that for all n n (1) 0 < b n. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). This cheat sheet is not intended to be a list of guaranteed rules to follow. If all the terms snare positive. If f(n) = sn, continuous, positive, decreasing: 2 series cheat sheet theorem (alternating series test). Then there exists a number c such that a < c < b and. P snconverges () r1 1. Let fb ngbe a sequence.
2 series cheat sheet theorem (alternating series test). If f(n) = sn, continuous, positive, decreasing: Let fb ngbe a sequence. If all the terms snare positive. Then there exists a number c such that a < c < b and. This cheat sheet is not intended to be a list of guaranteed rules to follow. P snconverges () r1 1. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). If there exists some n such that for all n n (1) 0 < b n.
2 series cheat sheet theorem (alternating series test). If all the terms snare positive. P snconverges () r1 1. If there exists some n such that for all n n (1) 0 < b n. This cheat sheet is not intended to be a list of guaranteed rules to follow. Then there exists a number c such that a < c < b and. Let fb ngbe a sequence. If f(n) = sn, continuous, positive, decreasing: Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ).
Sequences and Series Cheat Sheet Download Printable PDF Templateroller
Let fb ngbe a sequence. This cheat sheet is not intended to be a list of guaranteed rules to follow. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). Then there exists a number c such that a < c < b.
Calculus 2 Cheat Sheet
Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). If there exists some n such that for all n n (1) 0 < b n. This cheat sheet is not intended to be a list of guaranteed rules to follow. P snconverges.
Calculus 2 Cheat Sheet
Then there exists a number c such that a < c < b and. 2 series cheat sheet theorem (alternating series test). Let fb ngbe a sequence. If all the terms snare positive. This cheat sheet is not intended to be a list of guaranteed rules to follow.
Calculus formula sheet Cheat Sheet Calculus Docsity
P snconverges () r1 1. If there exists some n such that for all n n (1) 0 < b n. If f(n) = sn, continuous, positive, decreasing: 2 series cheat sheet theorem (alternating series test). Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f.
Calculus II Cheat Sheet Series Download Printable PDF Templateroller
Then there exists a number c such that a < c < b and. P snconverges () r1 1. 2 series cheat sheet theorem (alternating series test). If f(n) = sn, continuous, positive, decreasing: Let fb ngbe a sequence.
Calculus 2 Series And Sequences
Then there exists a number c such that a < c < b and. 2 series cheat sheet theorem (alternating series test). If all the terms snare positive. If there exists some n such that for all n n (1) 0 < b n. If f(n) = sn, continuous, positive, decreasing:
Series Tests Cheat Sheet
2 series cheat sheet theorem (alternating series test). Let fb ngbe a sequence. P snconverges () r1 1. If f(n) = sn, continuous, positive, decreasing: This cheat sheet is not intended to be a list of guaranteed rules to follow.
Calculus Cheat Sheet Formulas & Theorems
If all the terms snare positive. 2 series cheat sheet theorem (alternating series test). If there exists some n such that for all n n (1) 0 < b n. P snconverges () r1 1. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f (.
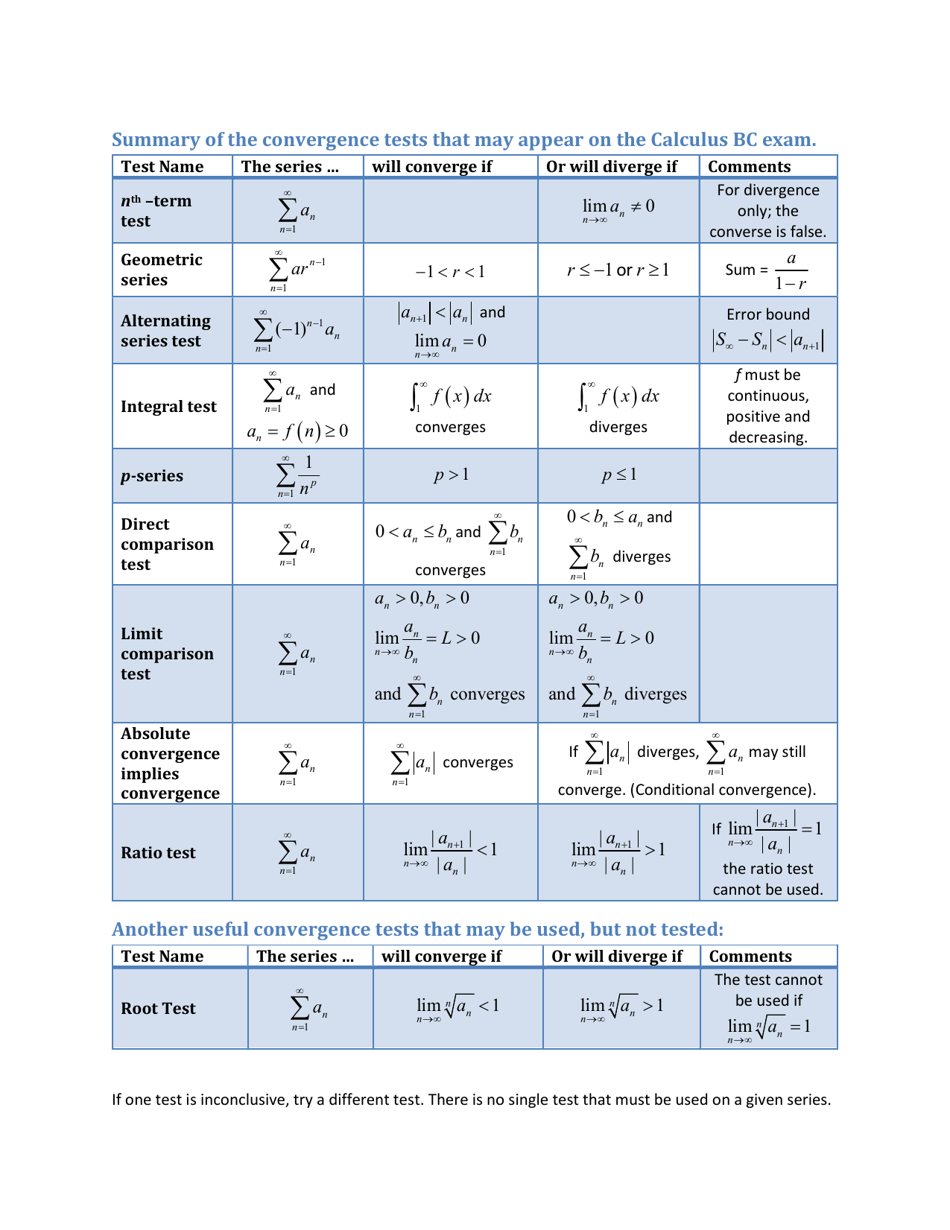
Calculus Bc Exam Series Convergence Tests Cheat Sheet Download
If all the terms snare positive. 2 series cheat sheet theorem (alternating series test). This cheat sheet is not intended to be a list of guaranteed rules to follow. Then there exists a number c such that a < c < b and. If there exists some n such that for all n n (1) 0 < b n.
Calculus 2 Cheat Sheet
If all the terms snare positive. Then there exists a number c such that a < c < b and. P snconverges () r1 1. If there exists some n such that for all n n (1) 0 < b n. Let fb ngbe a sequence.
Let Fb Ngbe A Sequence.
Then there exists a number c such that a < c < b and. If all the terms snare positive. 2 series cheat sheet theorem (alternating series test). This cheat sheet is not intended to be a list of guaranteed rules to follow.
P Snconverges () R1 1.
Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). If there exists some n such that for all n n (1) 0 < b n. If f(n) = sn, continuous, positive, decreasing: